Understand the interpretation of Othello
Discussion on the Othello GPT
This post is a personal analysis of a paper: Emergent World Representations: Exploring a Sequence Model Trained on a Synthetic Task.
Recently Li et al. applied mechanistic interpretation of GPT to Othello game
Probing Neurons
For a given neuron in a GPT model, the goal of probing is the verification of alignment between the concept and the activation of a neuron. Consider a set of neurons and the activations of several samples. When we assign labels on the activations, we can train a model to predict the relationship between activation patterns and the concepts.
Consider a set of activations over neurons for $N$ number of samples. When we stack them, we have the following form
\[\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_N \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & \cdots & a_{1d} \\ a_{21} & a_{22} & a_{23} & a_{24} & \cdots & a_{2d} \\ a_{31} & a_{32} & a_{33} & a_{34} & \cdots & a_{3d} \\ && \vdots \\ a_{N1} & a_{N2} & a_{N3} & a_{N4} & \cdots & a_{Nd} \\ \end{bmatrix}\]Linear
The linear probing assumes that there are linear relationship between the activation of a neuron and the label so that we can train a linear model with parameter \(\theta = \{ W \in \mathbb{R}^{d\times1} \}\). The function is the form of $y = Wa$.
\[\begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_N \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} & \cdots & a_{1d} \\ a_{21} & a_{22} & a_{23} & a_{24} & \cdots & a_{2d} \\ a_{31} & a_{32} & a_{33} & a_{34} & \cdots & a_{3d} \\ && \vdots \\ a_{N1} & a_{N2} & a_{N3} & a_{N4} & \cdots & a_{Nd} \\ \end{bmatrix} \cdot \begin{bmatrix} w_1 \\ w_2 \\ w_3 \\ w_4 \\ \vdots \\ w_d \end{bmatrix}\]With an assumption that the label is determined with boundary zero, the positive parameter $(\textcolor{red}{1})$ means the neuron maps the activation to label 1 and the negative parameter $(\textcolor{blue}{-1})$ means that the neuron maps the activation to label 2. Finally, the zero $(\textcolor{red}{0})$ means an invalid signal for classification.
Non-Linear
The Non-linear function assumes that the activation of neuron could be used to distinguish the concept in non-linear manner. In the Othello paper, the authors used the function:
\[f(x) = W_2 (\text{ReLU} (W_1))\]Intervention
Let $F$ be a GPT model and $G$ be a classifier for linear or non-linear probing. The proposed intervention modifies the activation of the GPT to change the classifier output to the different class. In Othello, let $x_t$ be the hidden representation at $t$-th token and $B$ is the current board state with $[x_1, \cdots, x_t]$. We have a desired board state $B’$ whose activation space are already known with classifier $G$. Then, we change the $x$ to the direction of the opponent label by gradient descent
\[\begin{equation} x' \leftarrow x - \alpha \frac{\partial \mathcal{L}_{CE}(G(x), B')}{\partial x} \end{equation}\]There are additional details about the intervention.
- The hidden representation is a key-vector
- The intervened token is in the last time step of $L \times T$ block.
- When the middle layer is intervened, all the upper layers are changed while the layer below unchanged.
What happens when middle layer is intervened:
Let’s assume that we have 8 layers and 5-th layer is intervened with Equation (1). After the activation is changed from $x_t^5$ to $(x^{‘})_t^{5}$ to align a concept to $B’$, the next layer computes $(x^{‘})_t^{6}$ with a transformer block. As the output may not align with the desired concept $B’$, it is further optimized with a classifier in the 6-th layer producing $(x^{“})_t^{6}$. The same procedure is applied to 7-th and 8-th layers.
Latent Saliency Attribution
The goal of LSA is to determine the contribution of previous tokens for the last prediction. That is, how the intervention of activations in the previous token will affect the logits of the current token whether increase or decrease the likelihoods.
Interpret the sign of $p_0 - p_s$ :
- (➕) Positive : As the probability decreased, the token was important for the prediction.
- (➖) Negative : As the probability increased, the token was not important for the prediction. (Note that the intervention changes the state of a tile to other class.)
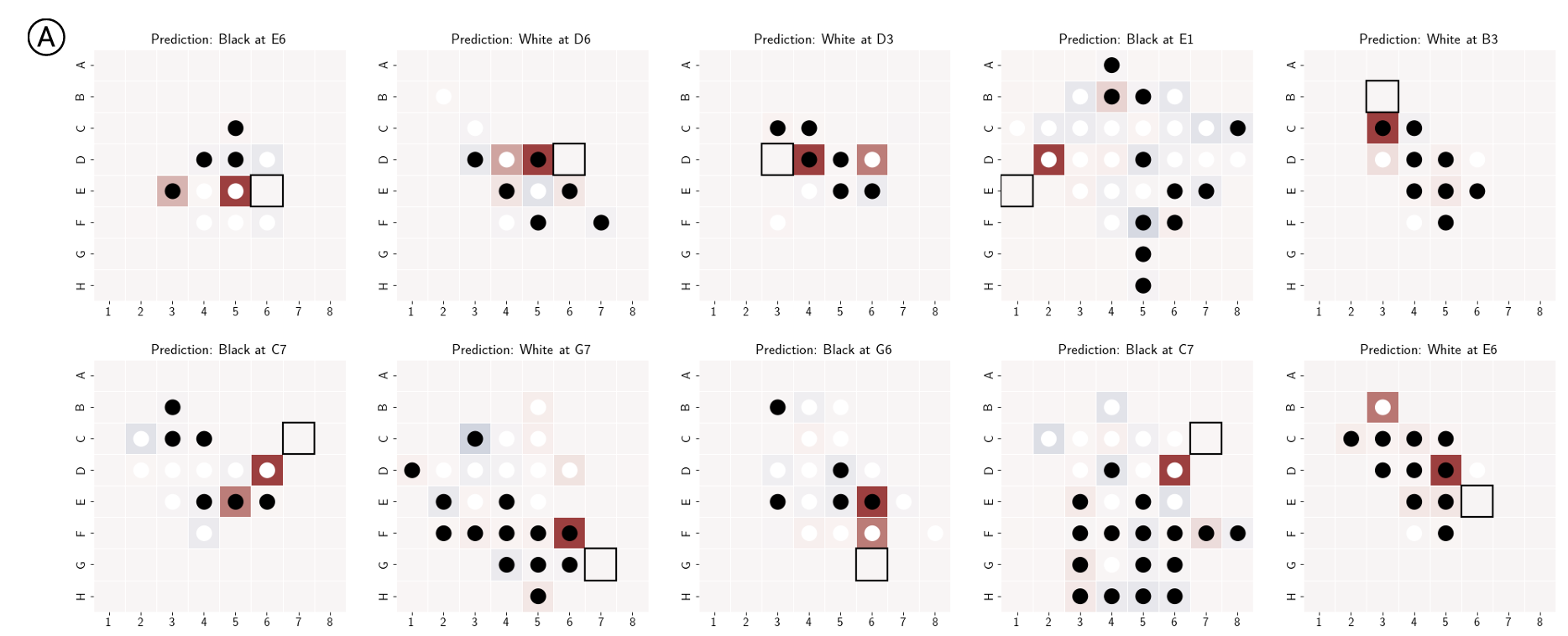
Figure. © Image from the [paper]. The bold solid square is the current prediction and the previous tokens are evaluated with LSA.
OthelloScope
- 1️⃣ How does a neuron affects logits over 60 tokens?
- 2️⃣ How do positions activate a neuron?
- 3️⃣ How can a neuron be used to separate a concept?
Figure. 2️⃣ How do positions activate a neuron 1201 in layer 1. © Image from [link].
See [OthelloScope].
Figure. (left and middle) 3️⃣ How can a neuron be used to separate a concept (left: my piece vs opponent, middle: black or not) (right) 1️⃣ logit lens for 60 tokens of neuron 79 in layer 6. © Image from [link]. See [OthelloScope].
The Geometriy of Probes
- Points : weights of the linear probing
- Edges: if the tokens are neighboring.
