2.1 Introduction to Transformer
📕 Chapter 2. GPT
Computational Interpretation of Circuits
Introduction
Interpretation of GPT is the most import task in deep learning to provide not only advanced but also reliable deep neural network. This article is about the interpretation of representations in GPT (transformer decoder-only model). Most of ideas in this post comes from A Mathematical Framework for Transformer Circuits, and we add some new thoughts to interpret the GPT.
The topics described in this article are as follows:
- 1. Streams : the stream of token representations over layers
- 2. Residual Spaces : communication between connected spaces.
- 3. Read and Write : interpret residual stream as read and write modules
- 4. Logit Lens : getting contribution of each block
- 5. Token Communication : information passing in tokens.
- 6. GPT Modules : description of basic modules in GPT : block, MLP, ATTN
- 7. Implementation : verify the forward passes of modules
- 8. Interpretability : find out where knowledge is stored
GPT : Causal Language Modeling
GPT is an autoregressive token generator.
Simplest : Embed and Unembed
The most simplest form of token generation is done by embedding the current token and unembed the next token.
— –>
2. Residual Spaces
Figure. Residual space image is obtained from A Mathematical Framework.
3. Read and Write
The input representation $x$ is encoded by a module $E_i:x\rightarrow r_i(x)$ and further added with the identity representation. The hidden representations $h_i$ where $i$ is the location of representation are as follows:
\[\begin{gather} h_0 = x \\ h_1 = x + r_1(x) \\ \Rightarrow h_2 = x + r_1(x) + r2(x + r_1(x)) \end{gather}\]4. Logit Lens
As all the representations are linearly added, we can decompose the contribution of each block or location. By combining the idea that the final hidden representation is further mapped to the vocabulary, we can factorize the logits of vocabulary as follows.
5. GPT Modules
6. Token Communication
The residual stream only combines representations of modules in a specific token stream. In other words, there is no communication between tokens if we don’t mix the representations. A way to mix representations in the transformer is the multi-head attention (MHA) pass information in each token weighted by attention scores.
- All the tokens will ask other tokens “how much information to give to the query”
- Each token will give value weighted by attention score (query * key)
Note that the stream of the query token will be replaced by values of other tokens unless query get higher attention to itself. For example, if the values of other tokens are noise, the attention score of itself should be high to mitigate the disturbance of noise.
Figure. Residual space image is obtained from A Mathematical Framework .
Multimodal Token Communication
The token communication is essential in text-to-image generation such as Parti Parti Google In multimodality, the values will be text representation which are injected to the stream of image representations.
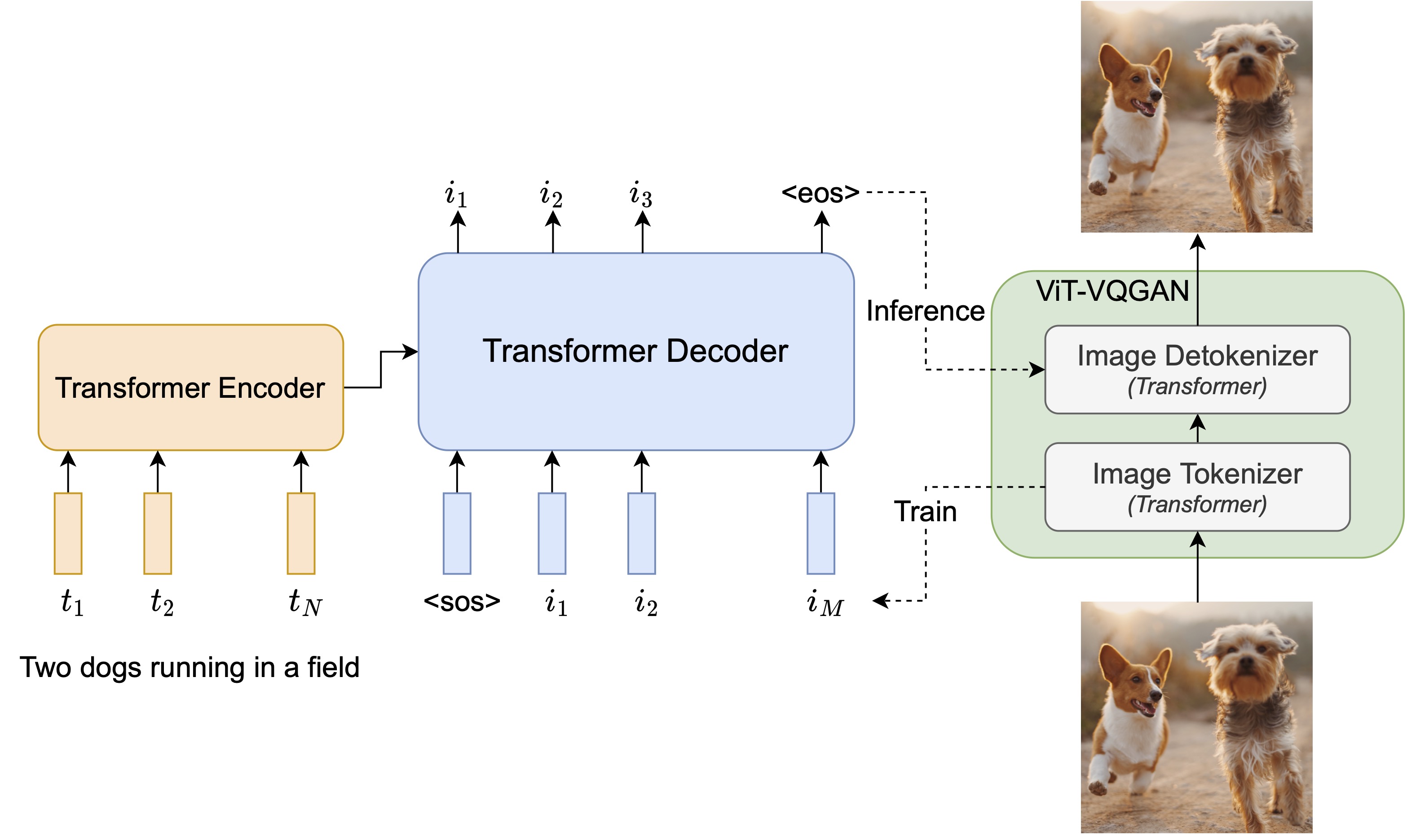
7. Implementations
8. Interpretability
How do the Transformer-based models perform well? How do they store the knowledge? We need to find out how they work, and there are some methods to make interpretations of predictions.
Knowledge Attribution
Figure. Knowledge Neurons in Pretrained Transformers Dai et al., 2022.
The feed-forward module is regarded as a key-value memory.
\[FFN(x) = f(x \cdot K^{\top})\cdot V \quad where\; K, V \in \mathbb{R}^{d_m \times d}\]In this context, we can try finding out which neurons in the FFN have knowledge of a specific prediction. The Knowledge Attribution method allows measuring the contribution of each neuron to prediction when performing a fill-in-the-blank cloze task. The attribution score of each neuron is defined as follows. $w_i^{(l)}$ denotes the $i$-th intermediate neuron in the $l$-th FFN.
\[Attr(w_i^{(l)}) = \bar{w}_i^{(l)} \int_{\alpha = 0}^{1} \frac{\partial P_x(\alpha \bar{w}_i^{(l)})}{\partial w_i^{(l)}}d\alpha\]Intuitively, as $\alpha$ changes from $0$ to $1$, by integrating the gradients, $Attr(w_i^{(l)})$ accumulates the output probability change caused by the change of $w_i^{(l)}$.
