Neurons in Deep Learning

How can we interpret neurons in deep learning?
[📚 Neuron Series 2]

Introduction

In the previous section, we introduced neurons in deep learning by comparing neurons in neuroscience. The previous section only introduced neurons in a linear weight and bias. With the same interpretation, we introduce several neurons in deep learning modules including multi layer perceptron (MLP), convolutional neural network (CNN), recurrent neural network, and generative pretrained models (GPT). In addition, we also provide a neuron perspective on key-value memory in GPT. We believe this interpretation of neurons can further help to understand the general computation of deep neural networks.

Linear Neurons in MLP

Let see the most basic module, weights in a linear layer. The weights are a matrix whose rows are the outputs for neurons and the columns for the synapses of these neurons. You can think that each row (neuron) computes independently the input signal $x$.

With the assumption that $W \in \mathbb{R}^{\textcolor{red}{m} \times \textcolor{blue}{n}}$

MLP is a series of linear neurons with activations in between them. The activations are thresholds to pass the information with valid signals. For example, ReLU cuts negative signals and Tanh provides gating mechanisms of signals. Therefore, in the interpretation of neurons, we can think of activations as modifiers of neurons’s outputs.

The Figure below shows two layer MLP. Each layer has two neurons and the neurons in the first layer have three synapses for each neuron, while the neurons in the second layer have two synapses for each neuron.

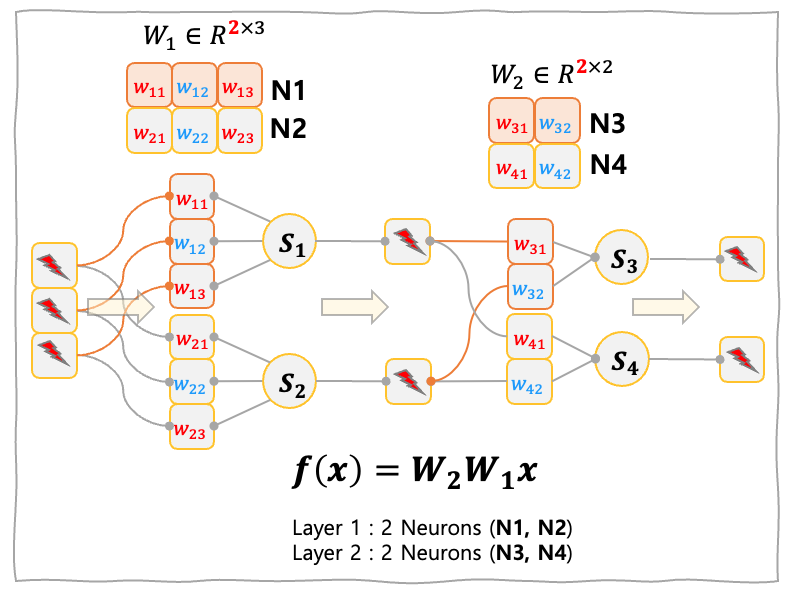
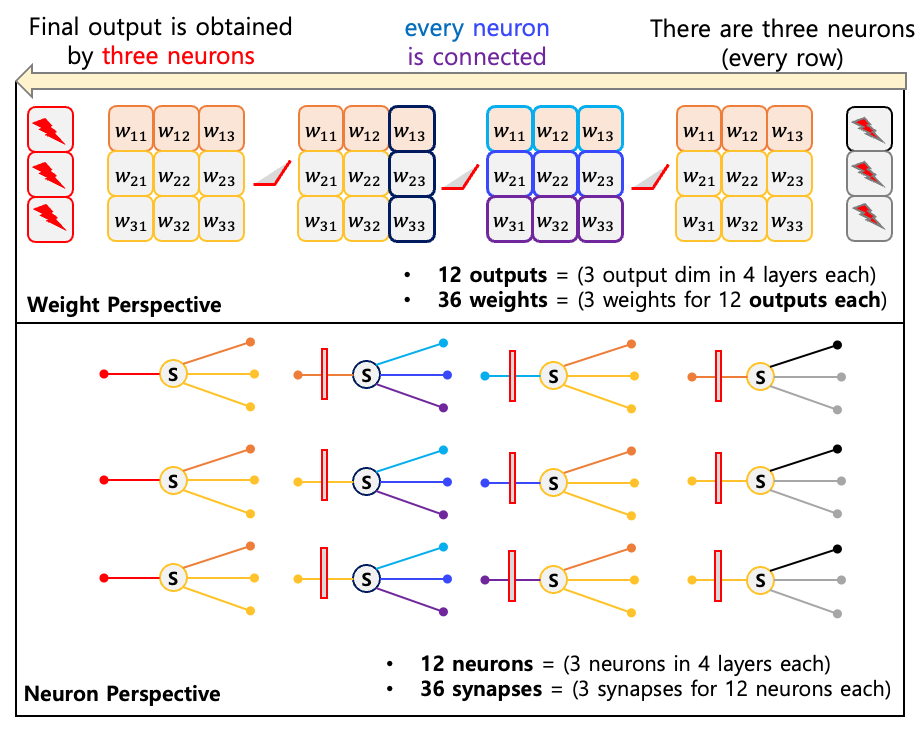
There are 2 neurons in each layer and 4 neurons in total. Synapses in a neuron computes dot-product with the input signals.

The Figure below shows the four layer MLP. In each layer, three neurons exist and each neuron has three synapses. Note that all the pre-neurons and post-neurons are connected with synapses. We think that is why MLP is called a densely connected neural network.

An example of four layer MLP. The first panel shows weight perspectives, while the second panel shows neuron’s perspective. Note that all the neurons output only a single scalar respectively.

Convolutional Neuron

Convolutional layer is also considered as a linear layer as we can reformulate the convolution operation as a linear operation. However, we use another tool to interpret the convolutional neuron. The most frequent way of creating a convolutional layer is using the notation: (out_channels, in_channels, kernel, kernel, ..). With this notation, the out_channels parts are the same with the rows in the linear neuron and (in_channels, kernel, kernel) are the synapses for a neuron. With this interpretation, the only difference with the linear layer is (kernel, kernel) part where the convolution operation is applied in the 2D plane. If you assume that kernel size is 1, then you can think of a linear neuron!

Recurrent Neuron

Beside MLP and CNN, the other basic module is a recurrent neural network (RNN) which successively computes an input with linear operations in it with hidden states. Computationally, the recurrent neuron is the same with the linear neuron except input and output types. Note that the recurrent neuron should provide outputs which are re-injected to the input of that neuron. The advanced RNN modules such as LSTM and GRU use the gating mechanism in them to process the long-term memory well. These architectures do not change the interpretation of neurons as they are combinations of linear neurons.

Neurons in GPT Block

Now we discuss neurons in more advanced architectures such as GPT. GPT consists of a token embedding module, transformer decoder blocks and task specific heads such as LMHead. We verify neurons in a GPT block and leave the interpretation of other modules as they are just linear-like neurons. GPT block has two main parts MLP and self-attention (or cross-attention), and layer-norm.

MLP

MLP block is a two layer MLP whose first layer is sometimes called key and second layer sometimes is called value. We use $d_{model}$ which is the dimension of GPT representations to describe the number of neurons and synapses. The key part is a linear layer with weight \(W_{key} \in \mathbb{R}^{\textcolor{red}{4\cdot d_{model}} \times \textcolor{blue}{d_{model}}}\) whose number of neurons is four times larger than the number of synapses. On the other hand the value part is a linear layer with weight \(W_{value} \in \mathbb{R}^{\textcolor{red}{ d_{model}} \times \textcolor{blue}{4\cdot d_{model}}}\) whose number of neurons is four times smaller than the number of synapses. Therefore, this architecture is a bottleneck architecture and many researchers interpret it as a neural memory.

Consider $d_{model} = 12,288$ which is the hidden dimension size of GPT3 (175B).

ATTN

In ATTN, there are four linear layers: query, key, value, output and each layer has weight \(W \in \mathbb{R}^{\textcolor{green}{d_{model}} \times \textcolor{green}{d_{model}}}\). Therefore, we can easily interpret neurons in ATTN If you assume QK, OV circuits, the number of neurons are reduce by 2 times. . Note that self-attention and cross-attention are about how to use these neurons and do not affect the interpretation of neurons

Consider $d_{model} = 12,288$ which is the hidden dimension size of GPT3 (175B).

Neurons in GPT3 (175B)

Finally, we count the number of neurons and synapses in GPT3 (175B) blocks with the above interpretation Caveats: We do not count the layer-norm in a block and the number of weights would not exactly match with the number of synapses in this case. Also, bias is a parameter in GPT, but is not counted for neuron and synapse. . GPT3 has 96 blocks and each block has MLP whose number synapses is 1,207,959,552 and ATTN whose number of synapses is 603,979,776. We can simply add these two and multiply 96 to compute the total number of synapses.

As humans have 7,000 synapses per neuron, we can think that GPT3 has a similar number or even larger number of connections between neurons. However, humans have much more neurons compared to GPT. We believe such a difference can affect the general learning process. For example, if the number of neurons is large, we can see them as an ensemble of simple knowledge. On the other hand, if the number of synapses is large, expert neurons will provide knowledge.

Conclusion

As we think more about a deep neural network with a metaphor to a human brain, the computational graph is highly interpretable and the individual components handle very simple computations like neurons in our brain. Recent work in interpretability is about discovering meanings of neurons and the work like this can shed light on the interpretation of the deep neural network. We believe still deep dissection of neural network can give better interpretation of deep neural networks.

(Appendix) Interpret Key Neurons and Value Neurons

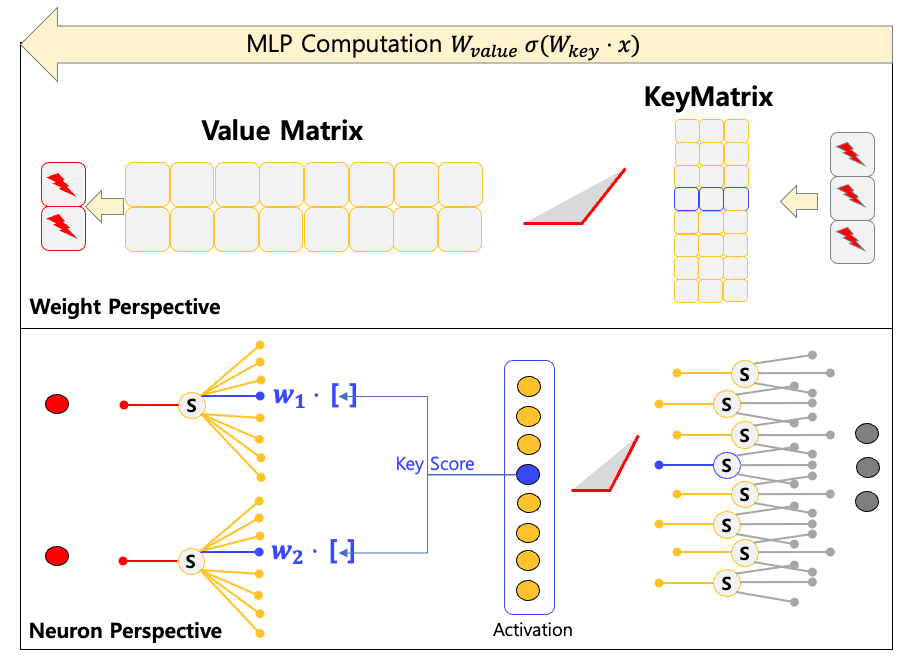
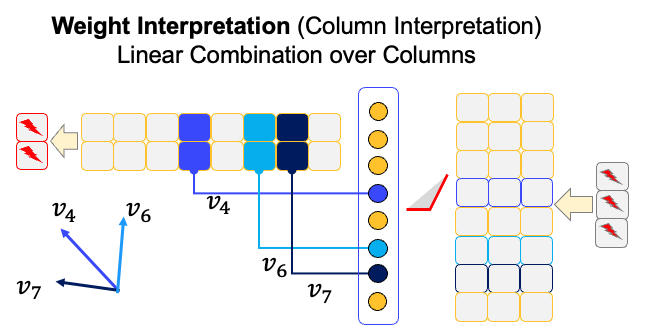
In the MLP section, we discuss the key-value neurons. In this section, we provide more detailed neuron-perspectives on these modules. The Figure below shows key-value computation with sizes, 3 for input, 8 for key, and 2 for value neurons We use 3 for the better visualization of the input, which is originally 2 in GPT. .

The key-neurons output scalars which are multiplied with weights (synapses) in the value-neurons. Then, the values neurons compute them (linear sum) to make a single output respectively.

If we just assume that a neuron just provide a single output, we can interpret a neuron in a row-wise manner. That is, we don’t think about the meaning of weights and just consider the output value of each neuron. The Figure below shows the neuron-wise interpretation.

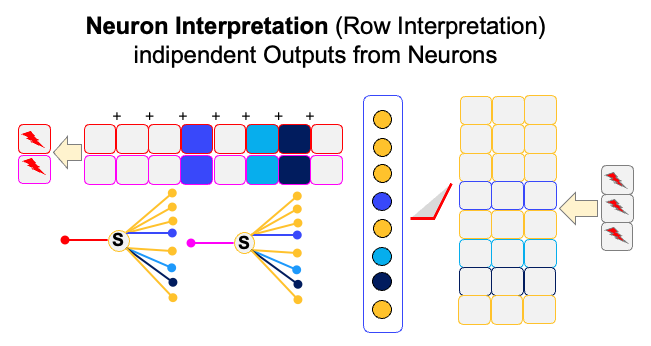
The row-wise neuron interpretation. As a single neuron has multiple synapses, the aggregated signal will go out and further be cut with activations.

Unlike the neuron-wise interpretation where we interpret each neuron separately, we usually interpret multiple neurons together by considering the directional vector. In this case, the weights in value-neurons are not just used for aggregation of synapses, but could be interpreted by directionally meaningful information. The Figure below shows the example. In this case, the key is used to scale the vectors.

Column-interpretation of neurons. It is more natural to think a weight matrix as directional vectors. The key-neurons output scales for the directional vectors.