1. Introduction

Evaluation of a pre-trained large models is essential to understand the properties of models. One of critical evaluations is the bias of a model for social groups which are also known as democratic axes. Examples are "gender, race, and community". On these democratic axes, there are words that the model should not bias to specific words. For example, when you ask a model:

"Who can be a nurse?"

Then, the likelihoods of words for the model output would be

LM's Answer : "woman: 0.7, man: 0.2, ..."

Even though the word "nurse" is highly entangled with the word "woman", The man should have similar probability with the woman as he could be a nurse too. Under this bias problem, we provide a quantitative analysis on the emergence of bias in the circuits of BERT. That is, we believe that the bias emerges at the internal representation of a model and we debias the layer to mitigate the bias. To this end, we propose several quantitative measures to understand the bias of BERT.

2. Bias Contribution of Layers

Measuring the contribution of layers is done with direct mapping of the hidden representations to the vocabulary. The direct mapping is possible as the blocks are connected by residual streams which refine the hidden representations. Figure below shows how logit-lens are related to the bias analysis. At the mask location, the prediction depends on the word Nurse which triggers bias of outputs. Note that every block outputs can be directly mapped to the vocabulary.

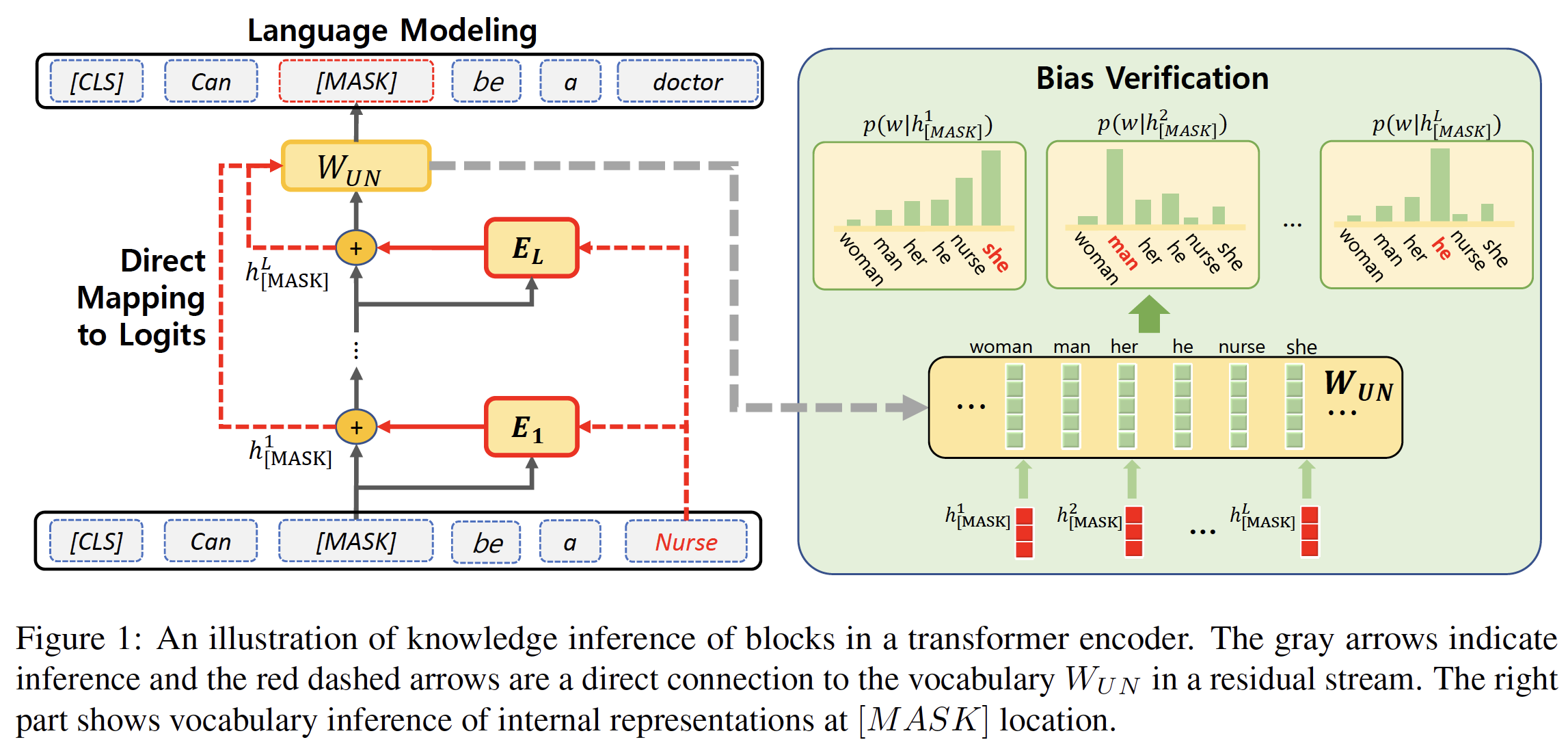
3. Measuring entropy of logits

To quantitatively measure the bias (imbalance of logits), we use entropy of probabilities over the democratic words such as $\{he, she, woman, man\}$ for Gender democratic axis. Figure below shows the entropy over attention modules and MLP modules over all layers. We observe that the emergences of imbalance are quite different for each democratic axis. In addition, MLP on [MASK] token has imbalance first than ATTN.

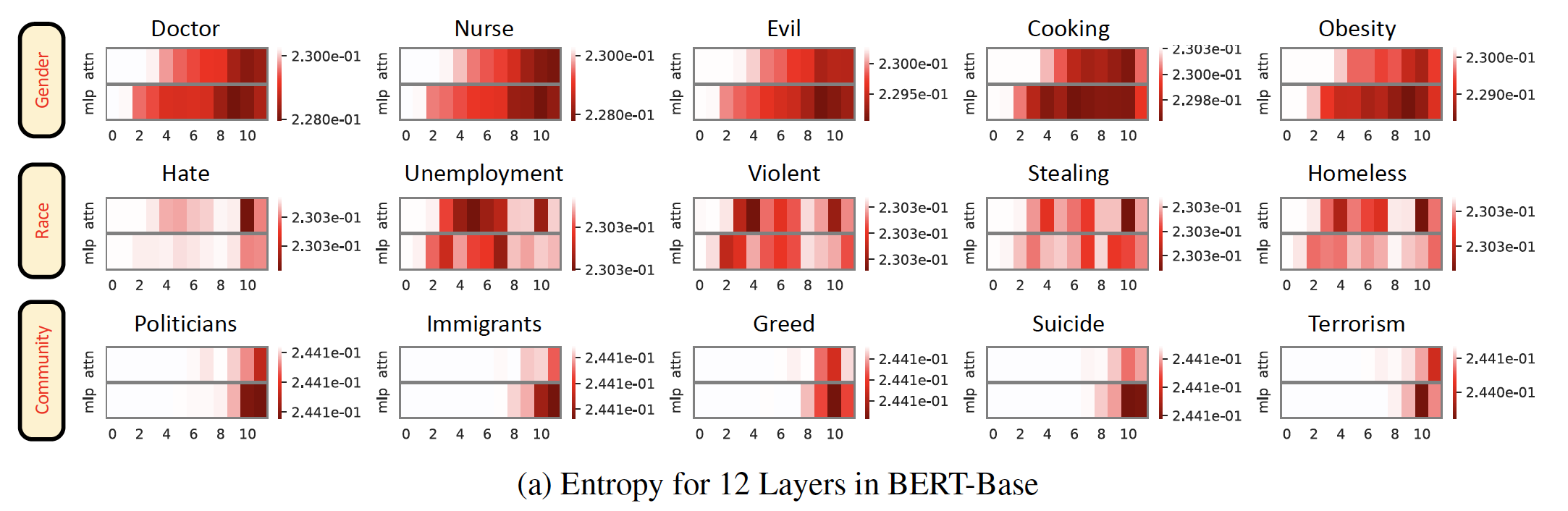
4. Masked Location Bias Scores

To blame the bias on the [MASK] token, we should verify whether the [MASK] position makes the bias or obtained the bias from other tokens. To measure the responsibility, we propose Masked Location Bias Scores (MLBs) which measures the difference of entropies of logit lens for MLP and ATTN at a block. Figure below shows the responsibility of bias.

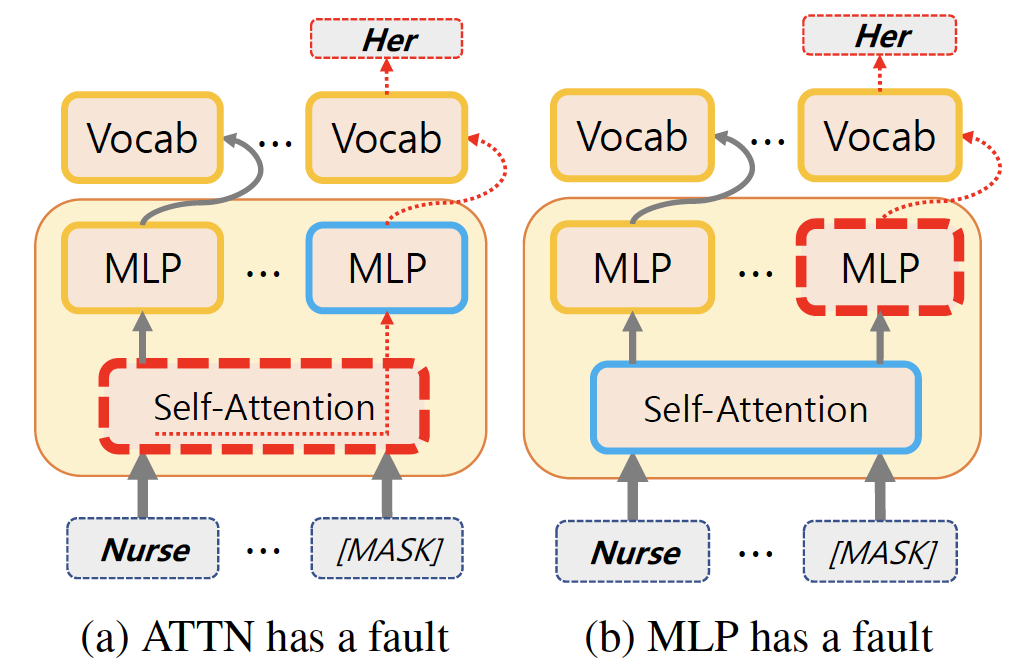
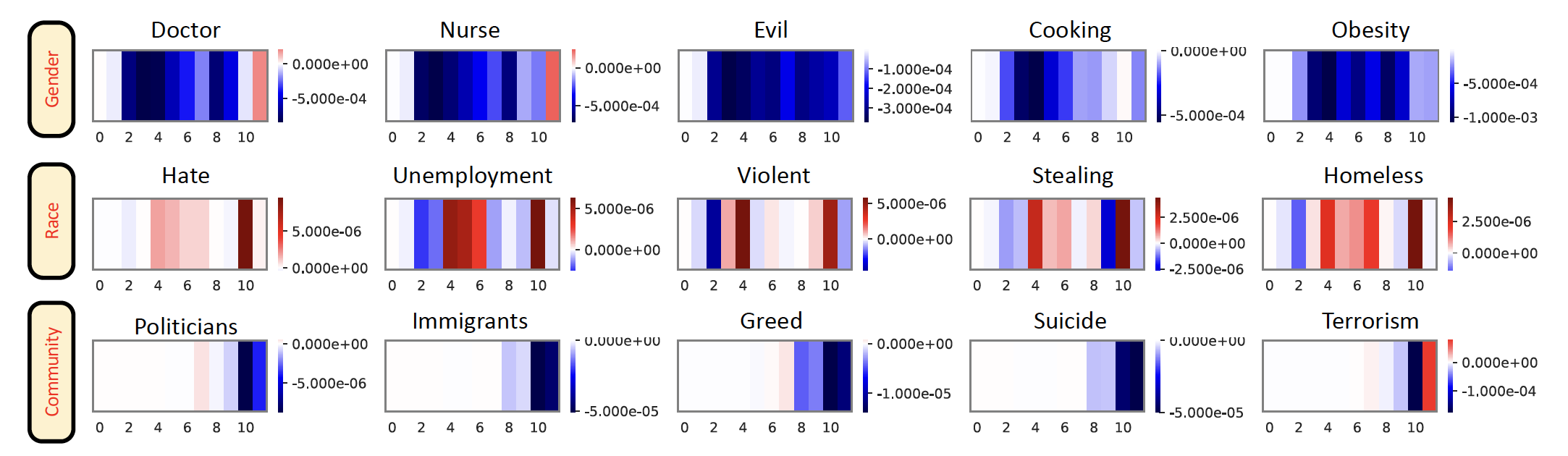
Figure below shows the MLBs over all layers. As color is close to red, the [MASK] location produces high bias than the bias obtained from other tokens. On the other hand, if the color is close to blue, the [MASK] location mitigate the bias.

5. What happens when debias?

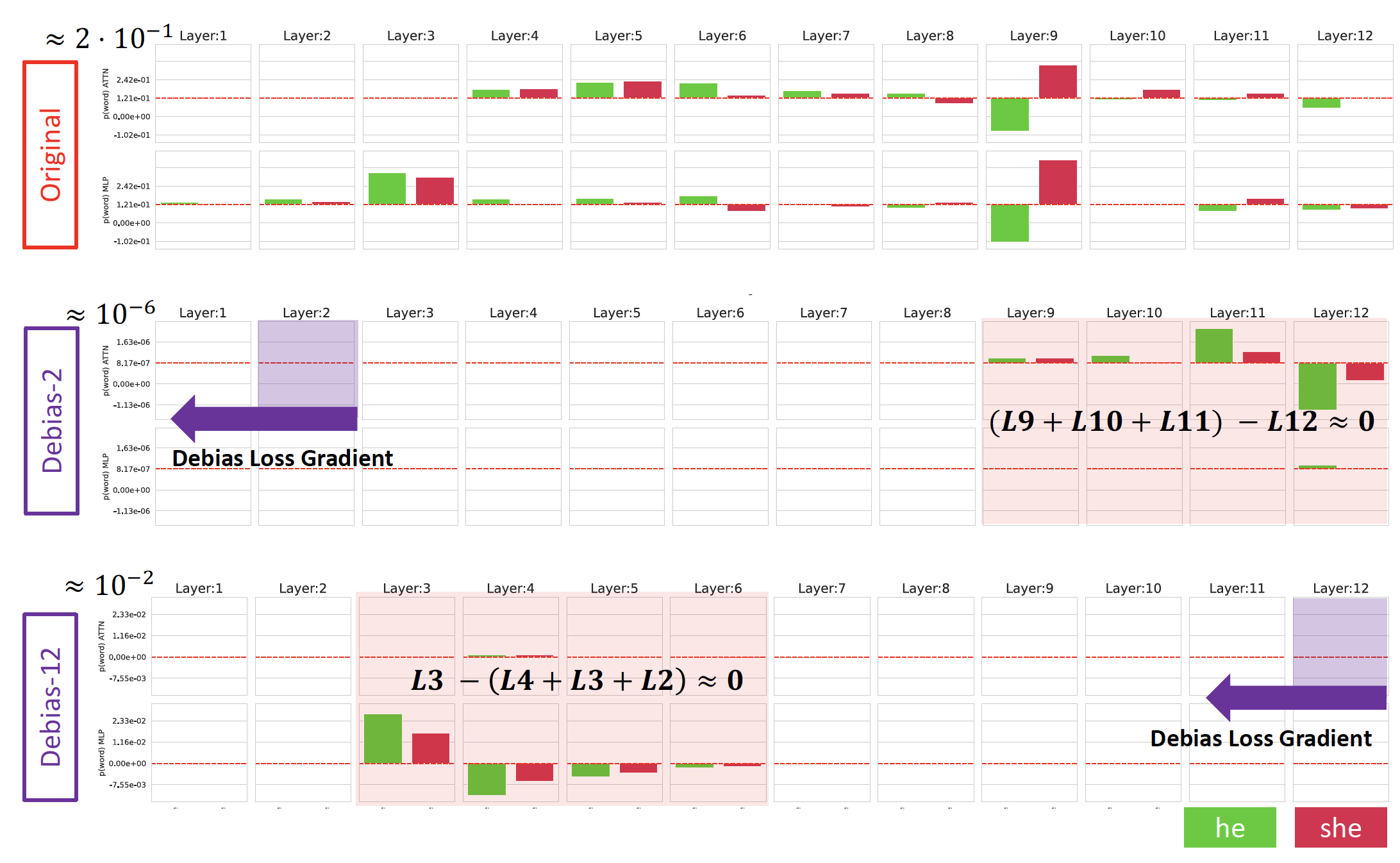
We conjecture that the bias of logit-lens for the selected layer only debias locally. That is, the logits of other layers are still biased. Figure below shows the marginal contributions of layers before debias and after debias. Note that when we select the debias location early, the logits of upper layers are still remaining. On the other hand, the debias of upper layers results in the survival of biases in the lower layers. One important observation is that they are sum to zero and the final output is also zero. Therefore, the observation (prediction) is debiased, while the internal layers still have biases.

Conclusion

We propose several quantitative analysis to understand biases in internal layers of BERT. We believe that understanding of internal biases is important to perfectly mitigate the bias of large models.