Memorizing Documents with Guidance in Large Language Models [IJCAI 2024]
Memorizing documents with known location of GPT is an urgent task for the reliable and faithful generation. This work proposes document guidance loss to disentangle document knowledge in LLM.
Paper Link: IJCAI Proceeding / Arxiv
- Code is available at Github🧑🏻💻
- This work is accepted at IJCAI 2024🍊
In AI, data plays a pivotal role in training. Large language models (LLMs) are trained with massive amounts of documents, and their parameters hold document contents. Recently, several studies identified content-specific locations in LLMs by examining the parameters.
Instead of the post hoc interpretation, we propose another approach, document-wise memories, which makes document-wise locations for neural memories in training. The proposed architecture maps document representation to memory entries and filters memory selections in the forward process of LLMs. Additionally, we propose document guidance loss, which increases the likelihood of text with document memories and reduces the likelihood with entries of other documents.
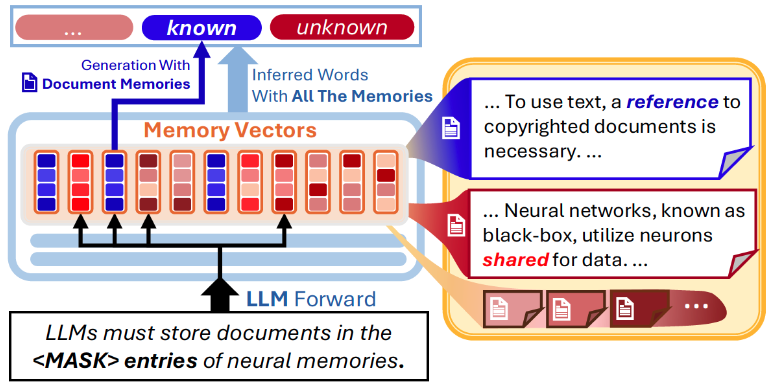
Document-Wise Memory
Document-wise Memory Structure
The document-wise memory entries have the following form. \(\begin{equation} \operatorname{MLP}_\mathrm{doc}(x) = V \Big( Key_\mathrm{Tok}(x) \odot Key_\mathrm{Doc}(\mathcal{K}) \Big) + b_v \end{equation}\)
The first key $ Key_\mathrm{Tok}(x)$ selects memories for the generation depending on the hidden representation $x$ in the language models. In contrast, the second key $ Key_\mathrm{Doc}(\mathcal{K})$ selects fixed entries of the memories for document $\mathcal{K}$.
Document Guidance Loss
To increase the likelihood of DocRep $\mathcal{K}$, the numerator part must be increased while the denominator part decreases. This is proportional to maximizing the following equation \(\begin{equation} P_\theta(y_t\vert y_{<t}; \mathcal{K}_i) - \alpha P_\theta(y_t \vert y_{<t} ) \end{equation}\) The loss $\mathcal{L}$ takes the following form \(\begin{equation} \mathcal{L} = \mathcal{L}_{CE}(\hat{y}^{\mathcal{K}_i}, y) + \alpha \vert \tau - \mathcal{L}_{CE}(\hat{y}^{\mathcal{K}^{-}}, y) \vert \end{equation}\) where \(\mathcal{L}_{CE}(\hat{y}^{\mathcal{K}}, y)\) is the cross entropy loss of passage $y$ and conditional generation $\hat{y}^{\mathcal{K}} \sim P_\theta(\cdot\vert \cdot, \mathcal{K})$. The right part is the forgetting loss with negative DocRep $\mathcal{K}^{-}$ and the expected loss $\tau$ for $P_{low}$. WLOG, we assume that $\tau$ is constant.
Memory Selection and Perplexity
Selected memories for documents have the following properties.
- The perplexity changes smoothly for the smooth change of the document representation.
- The activation plays an inductive bias in memory selection.
- The memory size correlates to the document length.
Measuring Separability
When recalling with document memories, ReLU and Tanh activations show how recall of the original document. Therefore, the trained memories stores more separable document contents!
Caveats of Nonlinear Memory Selection
More Dead Neurons
We observed that nonlinear memory selections do not work well with the proposed guidance loss. We compare 1 (linear case) to 4 layers with ReLU internal and final activations, adding $\mathrm{MLP}_\mathrm{Doc}$ after the last encoder layer. The models are trained with 10 documents, $\alpha=1.0, \tau=4.5$, and random negative DocReps. We observed dead neurons (not activated).
Quantitative Verification
To quantitatively evaluate memory selections, we train linear and nonlinear cases for five seeds and measure $L_0$, which is the number of non-zero entries, $L_2$ norm, and pairwise distance, which is $\Vert g(\mathcal{K}_i) - g(\mathcal{K}_j) \Vert _2$ for two DocReps $\mathcal{K}_i$ and $\mathcal{K}_j$, and normalized pairwise distance by $L_2$ norm of memory entries. All metrics are averaged over ten documents. The number of nonzero entries ($L_0$) increases for all cases, meaning the rank of memory usage increases. However, the normalized pairwise distance decreases as the layer depth increases. The linear memory provides more different memory entries than the nonlinear cases. The large gap between linear and nonlinear indicates the limitation of guidance loss with nonlinear cases.
Conclusion
Storing documents in the traceable locations of LLMs is a crucial research topic. This paper studies document-wise memories in LLMs. We propose document guidance loss to entangle document contents and document memories, encouraging different entries for documents. We also provide a theoretical view of memory selections with metric spaces and continuity assumptions. The experimental results show that the proposed guidance loss provides different memory entries with linear memory selection while leaving nonlinear memory selection as an open problem.
