
Paper
Github Code
(Becomes private on 2023.05.13 for a confidential issue)
Contributions
- We propose multi-robot task allocation framework with Mixed Integer Programming.
- We propose multi-robot task allocation framework with Markov Decision Process.
- We empirically show the gap between two formulation is less than 1 time step.
- We propose transformer-based allocation architecture.
- Our proposed transformer-based allocation architecture with reinforcement learning shows better performance than traditional allocation algorithms such as Genetic Algorithm and Greedy Algorithm.
Problem Definition
Consider ten rooms of different sizes in a building with five robot vacuum
cleaners ready at the battery-charging machine. In this setting, we want to allocate robots
to rooms such that all rooms are cleaned and the total elapsed time is minimized. If we
consider all possible allocations, there are $5 \cdot (10!)$ possibilities that we have to consider
for robots and permutations for ten rooms. This problem is an NP-hard problem, and
finding an optimal solution takes a long time.
However, instead of static allocation of robots, we can formulate it as a sequence of decision makings, that is, a Markov Decision Process (MDP). We want to allocate robots (actions) whenever there are ready robots during cleaning. Therefore, we formulate the problem hierarchically where the inner-environment is acting of robots and the outer-environment is handles an allocation of robots. This technique could be understood as temporal abstraction .
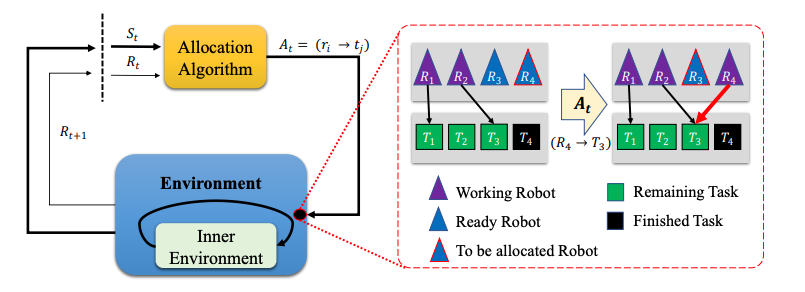
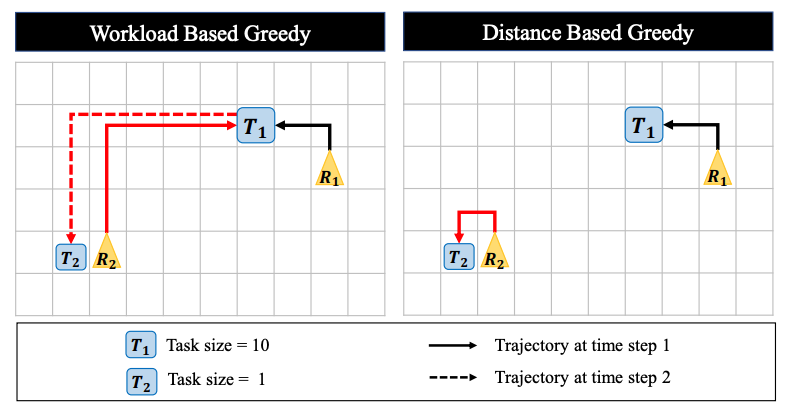
Greedy Algorithm is not optimal
To solve this sequential allocation problem, one traditional algorithm would be a greedy algorithm. The Figure below shows an example where there are two tasks $T_1, T_2$ and robots $R_1, R_2$. When we allocate robots based on the workload size, robot $R_2$ must travel long distance to work on $T_1$, and must return back to $T_2$ for the next work. Therefore, in this case distance based greedy allocation is better than workload based allocation.
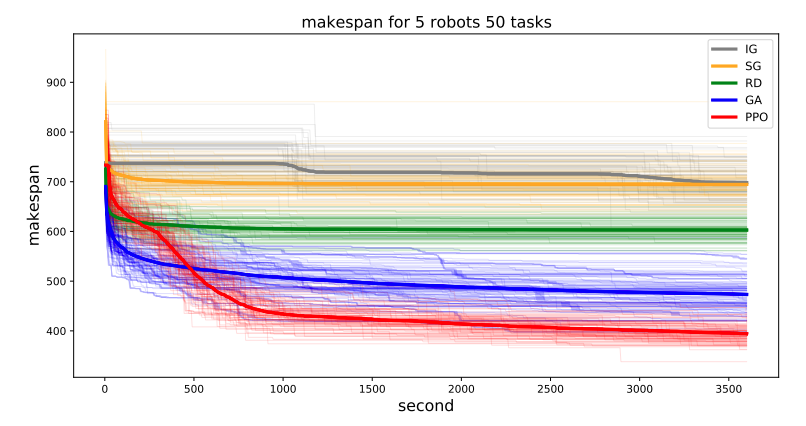
Allocation Performance
The Multi-robot Allocation problem is NP-hard problem and the traditional algorithm can not directly solve it. The traditional allocation solutions firstly generate a population of solutions and gradually update the solution for a given problem. Note that this task is not generalization problem, but rather finding the better solution with a limited time. For example, given a single allocation problem, find the best allocation way in 3500 seconds. This process requires 1) solution generation and 2) solution evaluation . The Figure below shows the makespan (time duration to finish the problem, smaller is better. )
- IG : iterative greedy algorithm which updates the solutions to better direction
- SG : stochastic version of the iterative greedy algorithm
- RD : random solution generation
- GA : genetic algorithm
- PPO : RL based allocation (Ours).
Transformer-based Architecture
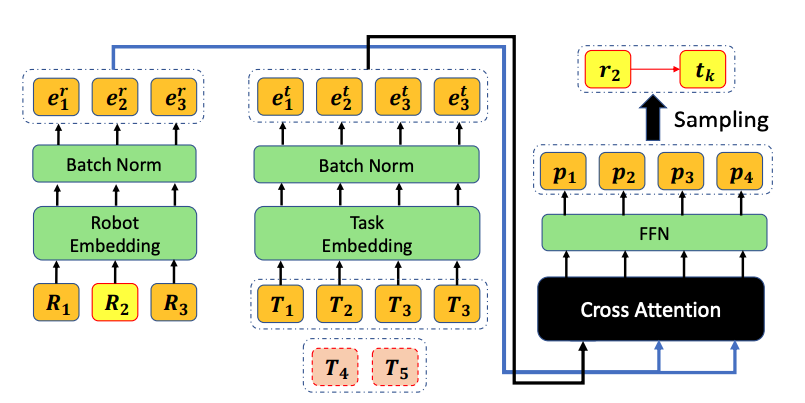
Now, I will describe the transformer-based architecture for allocation problem. The settings are as follows- We have a ready robot $r_i$ of our interest. (In Figure, $R_2$ )
- We have robot representations (location and states) and task representations (location and workload).
- Cross-Attention is used to get encode the robot information and decode the probability of tasks.
- We sample task which is maximized to return (sum of rewards in RL).
Limitation
If we visualize the allocation sequence for 5 robots and 50 tasks, the allocation does look optimal for human eyes. Even though the RL result has better performance than traditional methods, better representations for allocation must be developed.

bibliography
Park, Bumjin, Cheongwoong Kang, and Jaesik Choi. "Cooperative multi-robot task allocation with reinforcement learning." Applied Sciences 12.1 (2021): 272.
bibtex
@article{park2021cooperative,
title={Cooperative multi-robot task allocation with reinforcement learning},
author={Park, Bumjin and Kang, Cheongwoong and Choi, Jaesik},
journal={Applied Sciences},
volume={12},
number={1},
pages={272},
year={2021},
publisher={MDPI}
}